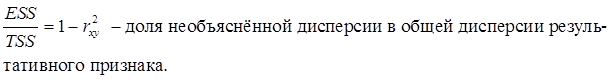Сущность МНК для парной регрессии состоит в минимизации суммы квадратов остатков (ESS – Error Sum of Squares).

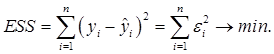
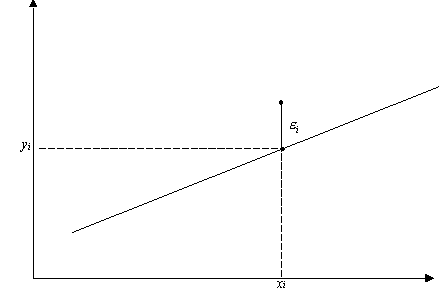
Наблюдаемое значение , положение модельной точки на линии регрессии и остаток показаны на приведеном ниже рис. 3.1.

y

x

Рис. 3.1

Учитывая, что параболы второй степени имеют один экстремум, отыщем ста­ционарную точку ESS как функции двух переменных a и b:

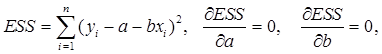
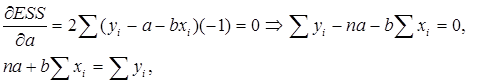
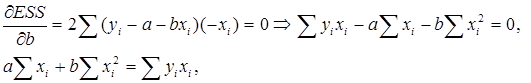
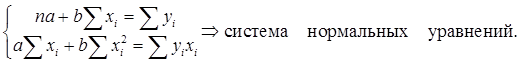
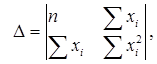
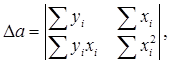
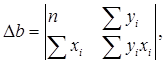
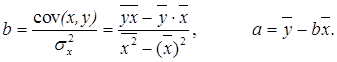
Параметр b – это коэффициент регрессии. Его величина показывает, на сколько единиц собственного измерения изменяется результат Y при изменении фактора на одну единицу собственного измерения;

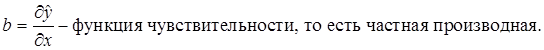
Свободный член a показывает совокупное влияние на результативный признак факторов, не учтённых в модели.

Уравнение регрессии почти всегда дополняют показателем тесноты статистиче­ской связи между случайными величинами X и Y. Для парной линейной регрессии это будет линейный коэффи­циент корреляции:

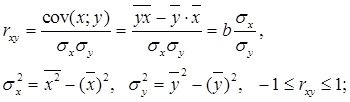
Корреляционная зависимость между двумя переменными – это функциональная зависимость между значениями одной из них и условным математическим ожиданием другой.

Коэффициент rxy оценивает тесноту связи рассмотренных при­знаков в её линейной форме, поэтому близость rxy к нулю не всегда означает отсутст­вие связи между признаками. При другой (нелинейной, специальной модели) связь между признаками может оказаться тесной.

Для оценки качества подбора линейных функций также рассчитывают коэффициент детерминации . Он характеризует долю дисперсии признака Y, объясненную рег­рессией, в общей дисперсии.
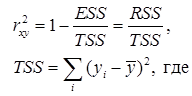
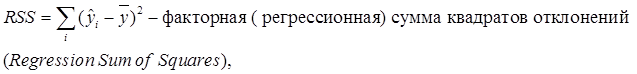
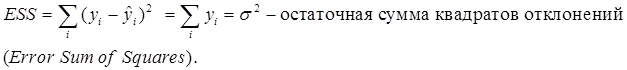