Для устранения гетероскедастичности или смягчения этой проблемы можно использовать так называемый взвешенный МНК (ВМНК). Рассмотрим ВМНК на примере парной регрессии:

.

Предполагается, что дисперсии остатков в каждом наблюдении нам известны. В качестве оценок дисперсии можно взять квадраты остатков в наблюдениях (единичных реализациях), так как математическое ожидание остатков в каждом наблюдении нулевое.

Разделим левую и правую часть уравнения на среднеквадратическое отклонение (СКО) остатка

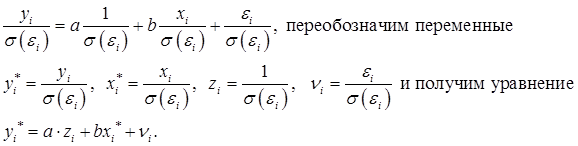Это уравнение регрессии без свободного члена, но с дополнительной объясняющей переменной zi. Покажем, что для выполняется условие гомоскедастичности:

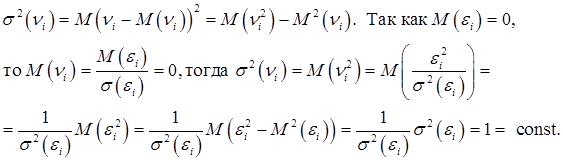
Если рассмотреть матричную форму записи модели множественной регрессии, то ВМНК будет сообразован с теоремой Айткена: в классе линейных несмещенных оценок вектора β для обобщенной линейной модели наиболее эффективна оценка

Если остатки гомоскедастичны, то есть Ωε = σ2I, то эффективной будет оценка

Ковариационную матрицу остатков при их гомоскедастичности (равноизменчивости) можно записать:

В случае с гетероскедастичностью эта матрица будет иметь вид

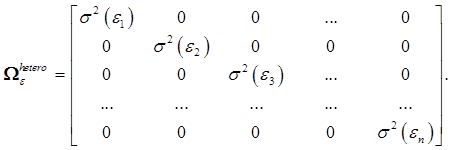
Ковариационные матрицы оценок для гомоскедастичного и гетероскедастичного случаев будут иметь вид

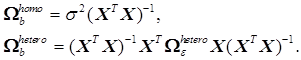
К сожалению, в большинстве случаев матрица Ω

ε точно не известна.

Иногда по результатам графического анализа гетероскедастичности можно увидеть, что Рассмотрим эти случаи на примере парной регрессии.

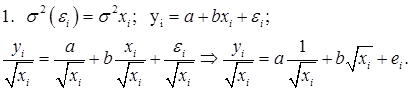
Для остатков будет выполняться условие гомоскедастичности, и можно будет к уравнению 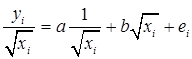применить классический МНК. Поясним это: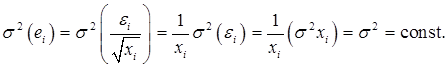

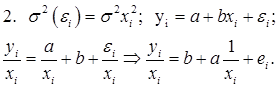
Для остатков будет выполняться условие гомоскедастичности, и можно будет к уравнению 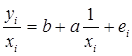применить классический МНК.

Действительно: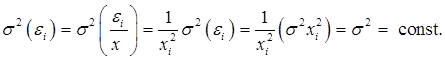

Для множественной регрессии можно рассмотреть версии , так как y есть линейная комбинация всех объясняющих переменных, и далее рассмотреть регрессию