В модели Койка предполагается, что в уравнении регрессии имеет место бесконечный лаг, но коэффициенты при лаговых переменных убывают в геометрической прогрессии, отсюда название – геометрическая структура Койка.

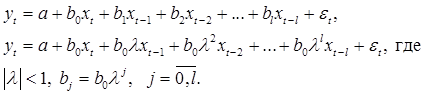
Последнее уравнение справедливо для всякого момента времени, в том числе и для момента ; поэтому можно записать

.

Умножим последнее уравнение на и вычтем из предыдущего:

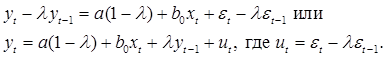
Краткосрочный мультипликатор рассчитывается как сумма бесконечно убывающей геометрической прогрессии

.

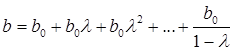Если считать, что объясняющая переменная стремится к равновесию , то значения и будут также стремиться к своему равновесному значению .

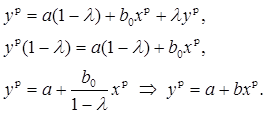
Здесь возможны следующие проблемы.

В уравнении регрессии регрессор в принципе носит случайный характер, так как содержит остаток , а значит, нарушается одна из предпосылок МНК. Для случайных остатков будет иметь место автокорреляция. Если учесть случайный характер регрессора и автокорреляция в остатках выражена достаточно сильно, то оценки параметров, полученные с помощью классического МНК, могут оказаться несостоятельными и смещенными.

Средний и медианный лаги модели Койка вычисляются таким образом:

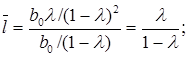
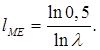
Видно, что если то . При ; при. Величину объясняют как скорость, с которой происходит во времени адаптация объясняемой переменной к изменению объясняющей переменной .