Сочетание авторегрессионного преобразования и скользящей средней называют ARMA–моделью (ARMA–autoregression & moving average model). Модель имеет вид

где ─ независимые друг от друга нормально распределенные случайные величины с нулевым матожиданием и постоянной дисперсией.

Преобразование ARMA в сочетании с переходом от объемных величин к приростным называется ARIMA–преобразованием или ARIMA–моделью (autoregression & integrated moving average model). Эту модель также называют моделью Бокса–Дженкинса.

В некоторых случаях такое преобразование позволяет получить более точную и явную модель зависимости. ARIMA-модель обычно используют для описания временных рядов со следующими свойствами: ряд аддитивно включает составляющую , имеющую вид полинома от t ; ряд, полученный из исходного ряда после применения к нему метода конечных разностей k раз, может быть описан моделью

.

Таким образом, модель может быть записана в виде

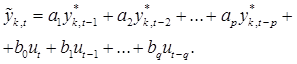
Величины представляют собой конечные разности порядка k переменной

В преобразованиях ARMA и ARIMA текущее значение yt переменной

Y выражается только через ее предыдущие значения и случайную составляющую (белый шум) ut.