Задание 3 ( косвенный МНК ).

По известной приведенной форме модели (ПФМ) построить с помощью КМНК структурную форму (СФМ). Далее, построить СФМ с помощью ДМНК и сравнить результаты. Для этого запишем приведенную форму модели и структурную форму модели в виде регрессионных уравнений. После этого используем косвенный метод наименьших квадратов (КМНК), для чего в правые части уравнений СФМ подставим выражения эндогенных переменных (у1, у2, у3), взятые из ПФМ.

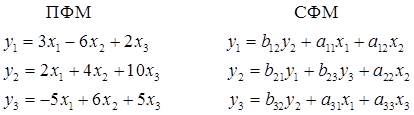
СФМ:

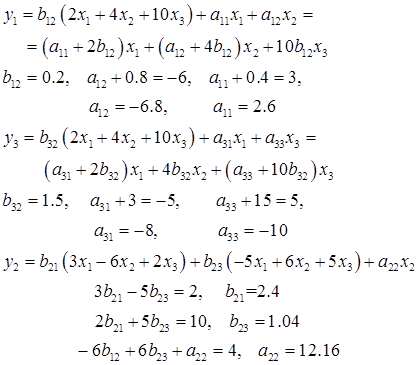
Запишем систему одновременных уравнений в виде СФМ с числовыми коэффициентами

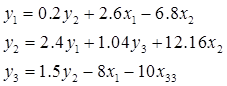
Теперь проверим правильность наших вычислений с помощью двухшагового метода наименьших квадратов (ДМНК). Для этого рассчитаем у1, у2, у3 по только что приведенным формулам и сравним с теми значениями, которые были получены с помощью инструмента «регрессия» по формулам ПФМ. Убедимся в идентичности значений. Следовательно, структурная модель построена корректно.

Проверка расчета по КМНК с помощью ДМНК